신경망 학습
학습이란 학습 데이터로부터 가중치 매개변수의 최적값을 자동으로 찾는것을 말한다.
✔︎ 훈련 데이터와 시험 데이터
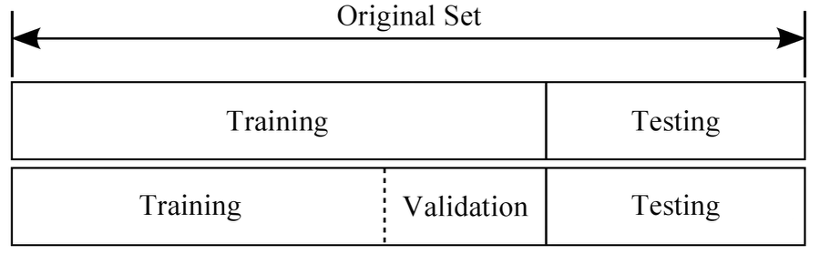
데이터를 훈련 데이터(training data)와 테스트 데이터(test data)로 나눠 학습과 테스트를 진행한다.
먼저, 훈련 데이터만 사용하여 학습하면서 최적의 파라미터(가중치, 편향)를 찾는다.
그런 다음 테스트 데이터를 이용하여 훈련된 모델의 성능을 평가한다.
과적합을 방지하기 위해 전체 데이터를 학습데이터, 검증데이터, 테스트데이터로 나누며 보통 비율은 5:3:2로 정한다.
- 학습데이터(training data) : 모형 f를 추정하는데 필요함
- 검증데이터(validation data) : 추정한 모형 f가 적합한지 검증함
- 테스트데이터(testing data) : 최종적으로 선택한 모형의 성능을 평가함
손실 함수 Loss Function
- 손실 함수란 신경망이 학습할 수 있도록 해주는 지표
- loss : 모델의 출력값과 사용자가 원하는 출력값의 차이, 즉 오차를 말한다.
- 손실 함수 값이 최소화되도록 하는 가중치와 편향을 찾는 것이 바로 학습이다.
1. 평균제곱오차 (Mean Squared Error : MSE)
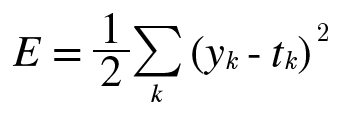

계산이 간편하여 가장 많이 사용되는 손실 함수이다.
기본적으로 모델의 출력 값과 사용자가 원하는 출력 값 사이의 거리 차이를 오차로 사용한다.
그러나 오차를 계산할 때 단순히 거리 차이를 합산하여 평균내게 되면, 거리가 음수로 나왔을 때 합산된 오차가 실제 오차보다 줄어드는 경우가 생긴다. 그렇기 때문에 각 거리 차이를 제곱하여 합산한 후에 평균내는 것이다. 위의 식에서는 1/2를 곱하는 것으로 되어 있으나 실제로는 2가 아닌 전체 데이터의 수를 나누어 1/n을 곱해주어야 한다.
- 거리 차이를 제곱하면 좋은 점은, 거리 차이가 작은 데이터와 큰 데이터 오차의 차이가 더욱 커진다는 점이다. 이렇게 되면 어느 부분에서 오차가 두드러지는지 확실히 알 수 있다는 장점이 있다.
- 회귀문제에 주로 쓰인다.
import numpy as np
# MSE 함수 구현
def mean_squared_error(y, t):
return 0.5 * np.sum((y - t)**2)
# 정답은 '2' -> one-hot
t = [0, 0, 1, 0, 0, 0, 0, 0, 0, 0]
# ex1) : '2'일 확률이 가장 높다고 추정함(0.6) -> softmax 결과값
y = [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0]
print('MSE of ex1 =', mean_squared_error(np.array(y), np.array(t)))
# ex2) : '7'일 확률이 가장 높다고 추정함(0.6)
y = [0.1, 0.05, 0.1, 0.0, 0.05, 0.1, 0.0, 0.6, 0.0, 0.0]
print('MSE of ex2 =', mean_squared_error(np.array(y), np.array(t)))
#
MSE of ex1 = 0.0975
MSE of ex2 = 0.5975
2. 교차 엔트로피 오차 (Cross Entropy Error : CEE)
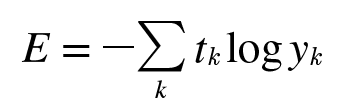

교차 엔트로피 오차는 기본적으로 분류(Classification) 문제에서 원-핫 인코딩(one-hot encoding)했을 경우에만 사용할 수 있는 오차 계산법이다.
위의 식에서 t값이 원-핫 인코딩된 벡터이고, 거기에다 모델의 출력 값에 자연로그를 취한 것이 곱해지는 형태이다.
결과적으로 교차 엔트로피 오차는 정답일 때의 모델 값에 자연로그를 계산하는 식이 된다.

- 분류 문제에서 모델의 출력은 0에서 1 사이이므로 -log(y)의 함수는 위와 같다.
즉, 정답이 1이라고 했을 때, 정답에 근접하는 경우에는 오차가 0에 거의 수렴해간다.
그러나 0에 가까워지면, 정답에 멀어지면 멀어질수록 오차가 기하급수적으로 증가하는 것을 볼 수 있다.
정답에 멀어질수록 큰 패널티를 부여하는 것이다.
- 일반적으로 분류 문제에서는 데이터의 출력을 0과 1로 구분하기 위하여 시그모이드(sigmoid) 함수를 사용한다.
시그모이드 함수 식에는 자연상수 e가 포함되므로 기존의 평균 제곱 오차를 사용하면, 매끄럽지 못하고 울퉁불퉁한 표면을 지닌
그래프의 개형이 그려진다. 이런 상태에서 경사 하강법(Gradient Descent Algorithm)을 적용하면 전역 최소점(global minimum)을 찾지 못하고 지역 최소점(local minimum)에 걸릴 가능성이 크다.
이것을 방지하기 위해 자연 상수 e에 반대되는 자연 로그를 모델의 출력 값에 취하는 손실 함수를 사용하는 것이다.
def cross_entropy_error(y, t):
delta = 1e-7 # log0 방지를 위함
return -np.sum(t * np.log(y + delta))
# 정답은 '2' -> one-hot
t = [0, 0, 1, 0, 0, 0, 0, 0, 0, 0]
# ex1) : '2'일 확률이 가장 높다고 추정함(0.6) -> softmax 결과값
y = [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0]
print('MSE of ex1 =', cross_entropy_error(np.array(y), np.array(t)))
# ex2) : '7'일 확률이 가장 높다고 추정함(0.6)
y = [0.1, 0.05, 0.1, 0.0, 0.05, 0.1, 0.0, 0.6, 0.0, 0.0]
print('MSE of ex2 =', cross_entropy_error(np.array(y), np.array(t)))
#
MSE of ex1 = 0.510825457099
MSE of ex2 = 2.30258409299
배치 Batch
배치는 한번에 여러개의 데이터를 묶어서 입력하는 것인데, GPU 의 병렬 연산 기능을 최대한 효율적으로 사용하기 위해 쓰는 방법이다.
➜ 배치는 GPU가 한번에 처리하는 데이터의 묶음을 의미
배치는 Iteration 1회당 사용되는 training data set 의 묶음이며, Iteration 은 정해진 batch size 를 사용하여 학습(forward - backward) 를 반복하는 횟수를 말한다.
미니배치 Mini-Batch
배치 작업보다 상대적으로 작은 단위로 처리하는 일괄처리이다.
미니배치는 데이터 처리의 효율을 높여주며 개별 학습 데이터의 특징을 무시하지 않으면서도 특징에 너무 휘둘리지 않게 해주어서 유용하다.

미니 배치 학습을 하게되면 미니 배치만큼만 가져가서 미니 배치에 대한 대한 비용(cost)를 계산하고, 경사 하강법을 수행한다.
그리고 다음 미니 배치를 가져가서 경사 하강법을 수행하고 마지막 미니 배치까지 이를 반복한다. 이렇게 전체 데이터에 대한 학습이 1회 끝나면 1 에폭(Epoch)이 끝나게 된다.
신경망은 최적의 가중치와 기타 파라미터를 찾기 위해서 역전파 알고리즘(backpropagation algorithm)을 사용한다.
역전파에는 파라미터를 사용하여 입력부터 출력까지의 각 계층의 weight을 계산하는 과정인 순방향과
반대로 거슬러 올라가며 다시 한 번 계산 과정을 거쳐 기존의 weight을 수정하는 역방향으로 나뉜다.
이 순방향과 역방향을 모두 완료하면 한 번의 Epoch가 완료됨을 의미한다. 더 쉽게 말하자면 1에폭은 학습에서 훈련 데이터를 모두 소진했을 때의 횟수에 해당한다.
딥러닝에서는 에폭 수나 미니배치 크기처럼 변경되지 않으면서 신경망 구조나 학습 결과에 영향을 미치는 고려 요인들을 하이퍼파라미터(hyper parameter)라고 한다. 하이퍼파라미터값은 신경망 설계자가 학습 전에 미리 정해주어야 하는 값이며 학습 결과에 큰 영향을 미치는 경우가 많다.
전체 데이터에 대해서 한 번에 경사 하강법을 수행하는 방법을 '배치 경사 하강법'이라고 부른다.
반면, 미니 배치 단위로 경사 하강법을 수행하는 방법을 '미니 배치 경사 하강법'이라고 부른다.
배치 경사 하강법은 경사 하강법을 할 때, 전체 데이터를 사용하므로 가중치 값이 최적값에 수렴하는 과정이 매우 안정적이지만, 계산량이 너무 많이 든다. 미니 배치 경사 하강법은 경사 하강법을 할 때, 전체 데이터의 일부만을 보고 수행하므로 최적값으로 수렴하는 과정에서 값이 조금 헤매기도 하지만 훈련 속도가 빠르다.
배치 크기는 보통 2의 제곱수를 사용합니다. ex) 2, 4, 8, 16, 32, 64...
그 이유는 CPU와 GPU의 메모리가 2의 배수이므로 배치크기가 2의 제곱수일 경우에 데이터 송수신의 효율을 높일 수 있다.
미분
경사법에서는 기울기 값을 기준으로 방향을 정한다.
미분을 사용하면 함수에 있는 어떤 점에서의 기울기를 알아보거나 순간적인 변화량을 구할 수 있다.
미분은 한 순간의 변화량을 계산한 것이다.

def numerical_diff(f, x):
h = 1e-4 # 0.0001
return (f(x+h) - f(x-h)) / (2*h)
편미분
편미분(partial derivative)은 다변수 함수의 특정 변수를 제외한 나머지 변수를 상수로 생각하여 미분하는 것을 말한다.
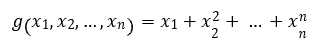
머신러닝에 나오는 최적화 문제에는 매개변수의 개수 만큼의 변수가 있으므로 목적함수가 이런 다변수 함수의 형태로 등장한다.
다변수 함수를 미분할 때는 미분할 변수에만 주목하고 다른 변수는 모두 상수로 취급해서 계산하는 편미분을 사용한다.
예시

합성함수 연쇄법칙
연쇄 법칙은 비용 함수의 결과로 얻은 오차를 기반으로 가중치를 조정하는 오차역전파(back propagation)을 이해하기 위한 사전 내용이다.
신경망의 각 계층마다 미분을 하는 변수가 다르기 때문에, 이를 위해서는 사용되는 법칙이 연쇄 법칙 이다.

연쇄법칙을 사용하면 임의의 식을 여러 개 끼워 넣어서 계산할 수 있다.
기울기 Gradient
모든 변수의 편미분을 벡터로 나타낸 것을 기울기(gradient)라고 한다.

기울기는 가장 낮은 장소를 가리키지만 각 지점에서 낮아지는 방향을 의미한다. 기울기가 가리키는 쪽은 각 장소에서 함수의 출력 값을 가장 줄이는 방향이라고 할 수 있다.

✔ 경사 하강법 (Gradient Descent)
최적의 파라미터(가중치, 편향) 즉, 손실함수가 최소가 되게 하는 파라미터를 찾기 위해 경사 하강법(Gradient descent)를 사용한다.
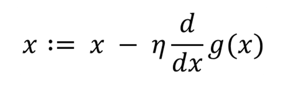
𝜂 는 업데이트하는 양을 나타내며, 학습률(learning rate)라고 한다.
한 번 학습할 때 얼마만큼 학습해야 하는지 학습 양을 의미하며 한 번의 학습량으로 학습한 이후에 가중치 매개변수가 갱신된다.
학습률 값은 미리 0.01, 0.001과 같이 특정 값을 정해두어야 하는 하이퍼 파라미터이며, 일반적으로 이 값이 너무 크거나 작으면 적합한 지점으로 찾아가기가 어렵다.
학습률이 너무 크면 큰 값을 반환하고, 너무 작으면 거의 갱신되지 않고 학습이 끝나버린다.

미분계수가 0인 지점을 찾는 방식이 아닌 gradient descent를 이용해 함수의 최소값을 찾는 주된 이유는
- 우리가 주로 실제 분석에서 맞딱드리게 되는 함수들은 닫힌 형태(closed form)가 아니거나 함수의 형태가 복잡해 (가령, 비선형함수) 미분계수를 계산하기 어려운 경우가 많다.
- 실제 미분계수를 계산하는 과정을 컴퓨터로 구현하는 것에 비해 gradient descent는 컴퓨터로 비교적 쉽게 구현할 수 있기 때문이다.
- 데이터 양이 매우 큰 경우 gradient descent와 같은 iterative한 방법을 통해 해를 구하면 계산량 측면에서 더 효율적으로 해를 구할 수 있다.
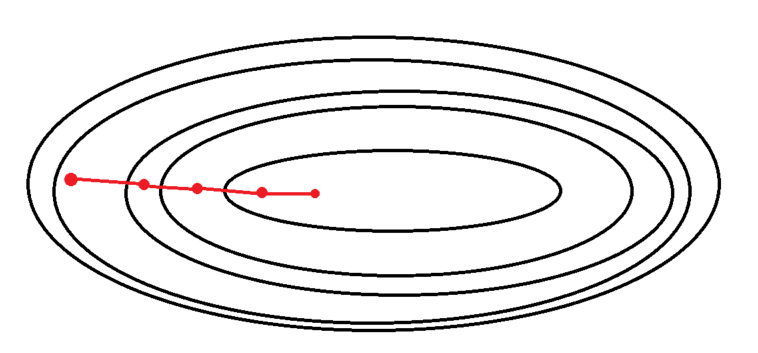
배치 경사 하강법 (Batch Gradient Descent: BGD)
배치 경사 하강법이란, 전체 학습 데이터를 하나의 배치로(배치 크기가 n) 묶어 학습시키는 경사 하강법이다.
➜ 전체 데이터 셋에 대한 에러를 구한 뒤 기울기를 한번만 계산하여 모델의 parameter 를 업데이트 하는 방법.
Gradient descent 라는 알고리즘 자체는 loss function 을 입력 데이터 x 에 대해 편미분해서 기울기를 계산하는 것이 아닌, 가중치 w 에 대해서 편미분을 하는 것이기 때문에, 기울기를 계산하는 것 자체는 입력 데이터 x 의 갯수와 상관이 없다.
전체 데이터에 대한 모델의 오차의 평균을 구한 다음, 이를 이용하여 미분을 통해 경사를 산출, 최적화를 진행한다.
보통 딥러닝 라이브러리에서 배치를 지정하지 않으면 이 방법을 쓰고 있다고 생각할 수 있다.
✔ BGD의 장점
- 전체 데이터에 대해 업데이트가 한번에 이루어지기 때문에 SGD 보다 업데이트 횟수가 적다.
따라서 전체적인 계산 횟수는 적다. (1 Epoch 당 1회 업데이트) - 전체 데이터에 대해 error gradient 를 계산하기 때문에 optimal 로의 수렴이 안정적으로 진행된다.
- 병렬 처리에 유리하다.
✔ BGD의 단점
- 한 스텝에 모든 학습 데이터 셋을 사용하므로 학습이 오래 걸린다.
- 전체 학습 데이터에 대한 error 를 모델의 업데이트가 이루어지기 전까지 축적해야 하므로 더 많은 메모리가 필요하다.
- local optimal 상태가 되면 빠져나오기 힘들다.
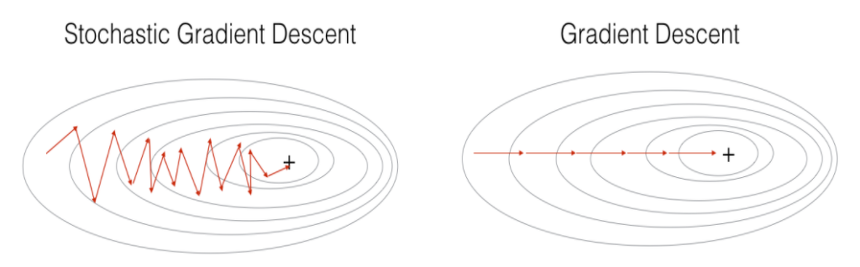
Stochastic gradient descent(SGD)
전체 데이터 중 단 하나의 데이터를 이용하여 경사 하강법을 1회 진행(배치 크기가 1)하는 방법이다.
전체 학습 데이터 중 랜덤하게 선택된 하나의 데이터로 학습을 하기 때문에 확률적 이라 부른다.
모델의 레이어 층은 하나의 행렬곱으로 생각할 수 있고, 여러개의 묶음 데이터는 행렬이라고 생각 할 수 있다.
즉, 여러개의 묶음 데이터를 특정 레이어 층에 입력하는 것은 행렬 x 행렬로 이해할 수 있는데,
SGD는 입력 데이터 한 개만을 사용하기 때문에 한 개의 데이터를 '벡터' 로 표현하여 특정 레이어 층에 입력하는 것으로 이해할 수 있고 이는 벡터 x 행렬 연산이 된다.
✔ SGD의 장점
- 위 그림에서 보이듯이 Shooting 이 일어나기 때문에 local optimal 에 빠질 리스크가 적다.
- BGD보다 계산량이 적다. (Batch Size에 따라 계산량 조절 가능)
- step 에 걸리는 시간이 짧기 때문에 수렴속도가 상대적으로 빠르다.
✔ SGD의 단점
- global optimal 을 찾지 못 할 가능성이 있다.
- 데이터를 한개씩 처리하기 때문에 GPU의 성능을 전부 활용할 수 없다.
Mini-batch gradient descent(MSGD)
딥러닝 라이브러리 등에서 SGD를 얘기하면 최근에는 대부분 이 방법을 의미한다.
SGD와 BGD의 절충안으로, 전체 데이터를 batch_size개씩 나눠 배치로 학습(배치 크기를 사용자가 지정)시키는 것이다.
예를 들어, 전체 데이터가 1000개인 데이터를 학습시킬 때, batch_size가 10이라면, 전체를 10개씩 총 100묶음의 배치로 나누어 1 Epoch당 100번 경사하강법을 진행한다.
Shooting이 발생하기는 하지만, 한 배치의 손실값의 평균으로 경사하강을 진행하기 때문에, Shooting이 심하지는 않다.

✔ MSGD의 장점
- BGD보다 local optimal 에 빠질 리스크가 적다. (Shooting이 적당히 발생)
- BGD보다 계산량이 적다. (Batch Size에 따라 계산량 조절 가능)
- SGD보다 병렬처리에 유리하다.
- 전체 학습데이터가 아닌 일부분의 학습데이터만 사용하기 때문에 메모리 사용이 BGD 보다 적다.
✔ MSGD의 단점
- batch size(mini-batch size) 를 설정해야 한다.
- 에러에 대한 정보를 mini-batch 크기 만큼 축적해서 계산해야 하기 때문에 SGD 보다 메모리 사용이 높다.
Batch Size 정하기
- Batch Size는 보통 2의 n승으로 지정
- 가능하면 학습데이터 갯수에 나누어 떨어지도록 지정하는 것이 좋은데, 마지막 남은 배치가 다른 사이즈이면 해당 배치의 데이터가 학습에 더 큰 비중을 갖게 되기 때문이다. ➞ 보통 마지막 배치의 사이즈가 다를 경우 이는 버리는 방법을 사용한다.
<참고 사이트>
1번 : light-tree.tistory.com/133
2번 : skyil.tistory.com/68
3번 : excelsior-cjh.tistory.com/170?category=940400
'DL(Deep-Learning) > 개념' 카테고리의 다른 글
| 활성화 함수 activation function (0) | 2022.01.29 |
|---|---|
| [실습] numpy로 만드는 단층 신경망 - 회귀 문제 (0) | 2022.01.29 |
| [DL] 오차 역전파 Error Backpropagation (0) | 2022.01.28 |
| [DL] 퍼셉트론(Perceptron) (0) | 2022.01.28 |
| 인공지능이란? (0) | 2022.01.28 |
![[DL] 신경망 Neural Network](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2Fcpxvbb%2FbtrslV4OswI%2FAAAAAAAAAAAAAAAAAAAAAMd7zy_AJy2UQWd6BoTHjjUqsM7GN76pL2HogIDr0_E7%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1764514799%26allow_ip%3D%26allow_referer%3D%26signature%3DhzfbAEz16BdK81jXB3uUO3AdHPw%253D)