엔트로피 Entropy
원래 분자들의 무질서도 혹은 에너지의 분산 정도를 나타내는 물리학 용어에서 출발한다.
정보이론에서의 Entropy
1948년 미국의 수학자이자 전기공학자인 클로드 섀년(𝐶𝑙𝑎𝑢𝑑𝑒 𝐸𝑙𝑤𝑜𝑜𝑑 𝑆ℎ𝑎𝑛𝑛𝑜𝑛)은 엔트로피 개념에서 힌트를 얻어 확률 분포의 무질서도나 불확실성 혹은 정보 표현의 부담 정도를 나타내는 정보 엔트로피(섀년 엔트로피) 개념을 고안해 낸다.
'정보‘라는개념이 등장하게 되는데, '정보이론'은 신호에 존재하는 '정보의 양'을 측정하는 이론이라 할 수 있다.
여기서 '정보의 양' 은 '놀람의 정도'를 의미한다. 놀람의 정도는 쉽게 말해 모두가 알만한 정보가 아닌, 새롭고 특이해서 사람들로 하여금 놀람을 일으키는 정도라고 이해하면 된다.
예를들어 '3년 뒤 삼성전자의 주식이 오른다’ 라는 정보는 대부분의 사람들이 알만한 정보니 정보량이 적고, ‘일론 머스크가 로켓을 쏘아 올린다’ 라는 정보는 놀라움을 주는 정보이니 정보량이 크다 라고 할 수 있다.
는 가 발현될 확률. 는 의 정보량이라고 하면,
- 불확실성이 클수록 정보량이 크다: $P(x_1) > P(x_2) => I(x_1)<I(x_2)$
- 두 개의 별건의 정보량은 각 정보량의 합과 같다: $I(x_1,x_2)=I(x_1)+I(x_2)$
여기서 두 개의 독립적인 사건 , 의 발생 확률은 $P(x_1)∗P(x_2)$인데, 정보량은 합산이기 때문에 이를 만족시키는 것은 를 씌우는 것입니다. 즉, $ I(x)=log_{2}\frac{1}{P(x)}$ 이 됩니다. - 정보량은 bit로 표현된다: $ I(x)=log_{2}\frac{1}{P(x)}$
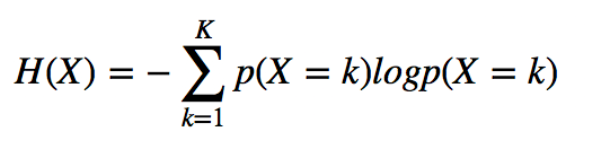
정보 엔트로피는 어떤 확률 분포로 일어나는 사건을 표현하는 데 필요한 정보량이다.
이 값이 커질수록 확률분포의 불확실성 또는 놀람의 정도가 커지게 되며 결과에 대한 예측이 어려워 지게 된다.
✔︎ 교차 엔트로피 Cross Entropy
정보 엔트로피는 하나의 확률분포가 갖는 불확실성(놀람의 정도) 혹은 정보량을 정량적으로 계산할 수 있게 하는 개념이다.
교차 엔트로피(Cross Entropy)는 두 가지 확률분포가 얼마나 비슷한지를 숫자 하나로 나타내는 개념이다.
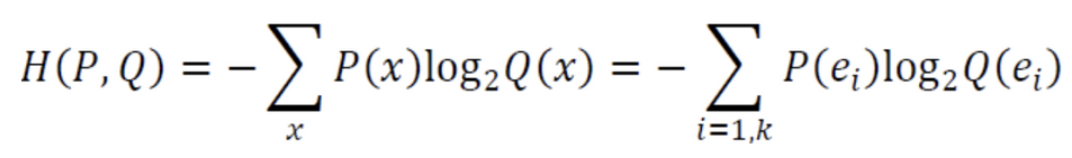
위의 식을 정리해보면,
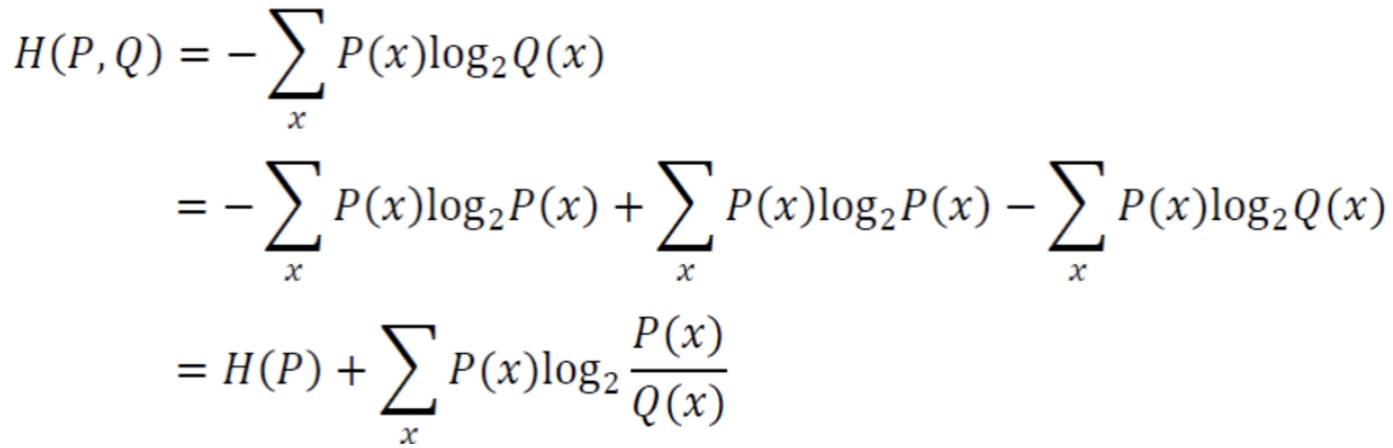
'틀릴 수 있는 정보($-log_{2}Q(x)$)를 가지고 구한 엔트로피($P(x)$)’ 즉 정보량 이다.
틀릴 수 있는 정보란 예를들어 딥러닝의 예측 결과라고 할 수 있다.
교차 엔트로피의 특징은 만약 딥러닝의 예측이 완전히 빗나가게 되면 교차 엔트로피값은 무한대가 되지만, 반대로 어느정도 학습이 된 경우라면 교차 엔트로피의 값은 엔트로피 값으로 수렴한다.
학습이 완벽하게 진행된 경우라면 교차 엔트로피와 엔트로피는 같은 값을 갖게 된다.
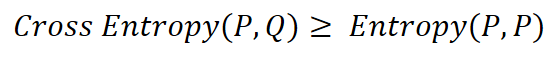
그래서 이러한 교차 엔트로피는 두 확률분포가 서로 얼마나 다른지를 나타내주는 정량적 지표 역할을 수행한다.
여기에 딥러닝 학습을 수행하는데 있어 딥러닝 모델의 추정 확률분포 Q, 그리고 딥러닝 모델이 추구해야 할 미지의 확률분포 P가 있다. 이 P와 Q를 활용하여 교차 엔트로피를 계산하며, 이 교차 엔트로피가 낮아지는 쪽으로 모델의 추정 확률분포 Q를 꾸준히 개선함으로 확률분포 Q를 확률 분포 P에 가깝게 접근시켜 갈 수 있다.
바로 이 점이 이진판단에서의 신경망을 학습시킬 수 있는 원리가 된다.
'DL(Deep-Learning) > 개념' 카테고리의 다른 글
| [실습] numpy로 만드는 단층 신경망 - 이진 분류 1 (0) | 2022.01.29 |
|---|---|
| train/test/validation 나누기 - splitfolders (0) | 2022.01.29 |
| 분류 성능 지표 - Precision(정밀도), Recall(재현율) (0) | 2022.01.29 |
| 활성화 함수 activation function (0) | 2022.01.29 |
| [실습] numpy로 만드는 단층 신경망 - 회귀 문제 (0) | 2022.01.29 |
![[DL] 엔트로피 Entropy](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FbDT78s%2FbtrsaTAWDND%2FAAAAAAAAAAAAAAAAAAAAALZDx64ADzEsvau3kVYSpnBUJfugkFnJ9mW5jASYBbjP%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1764514799%26allow_ip%3D%26allow_referer%3D%26signature%3DuvHm0k%252Be3G1qB7DhIgJqVRozoqs%253D)