이번에는 다중 분류를 위한 신경망을 만들어보려 한다.
이진 분류가 두 개의 선택지 중 하나를 고르는 문제였다면, 세 개 이상의 선택지 중 하나를 고르는 문제를 다중 클래스 분류라고 한다.
다중 분류 신경망은 이진 분류에서 처럼 일단 각 후보 항목에 대한 로그 척도의 상대적 추천 강도, 즉 로짓값을 추정하도록 구성된다. 이때 퍼셉트론 하나가 후보 하나에 대한 로짓값을 출력하게 된다. 따라서 다중 분류를 수행하려면 다중 분류 후보 수 만큼의 퍼셉트론이 필요하게 된다.
우선 로짓값은 상대적인 가능성을 로그를 이용해 나타낸 값이라 할 수 있다. 그리고 다중 분류에서 로짓값의 표현 대상은 각 후보 항목을 답으로 추정할 확률이 된다.
로짓값을 확률로 변환하지 않고서도 어떤 후보가 더 큰 값을 갖고 있는지 알 수 있는데 왜 확률로 값을 변환 할까?
딥러닝 문제를 수행하는데 있어 가장 큰 요인은 바로 '학습‘ 이다.
로짓값은 이러한 학습을 수행하는데 있어 마땅한 학습 방법을 찾기가 힘들었다. 확률분포와 교차 엔트로피 개념이 더해지게 되어 학습을 할 수 있는 방법를 찾게 된다. 신경망이 추정한 확률 분포와 정답이 나타내는 확률 분포 사이의 교차 엔트로피를 구할 수가 있으며, 이 교차 엔트로피를 손실함수 삼아 학습을 수행하게 되면 신경망이 연산한 값을 바탕으로 출력한 확률 분포, 즉 선택은 점점 정답에 근접 시킬 수 있게 된다.
다수의 후보 항목들에 대한 로짓값 벡터를 확률 분포 벡터로 변환해주는 함수 '소프트맥스(𝑠𝑜𝑓𝑡𝑚𝑎𝑥)'와 이렇게 구해진 확률 분포와 정답에 나타난 확률 분포 사이의 교차 엔트로피를 계산해주는 함수 '소프트맥스 교차 엔트로피(𝑠𝑜𝑓𝑡𝑚𝑎𝑥 𝑐𝑟𝑜𝑠𝑠 𝑒𝑛𝑡𝑟𝑜𝑝𝑦)' 가 필요하게 됩니다.
Softmax 함수
로짓값 벡터를 확률 분포 벡터로 변환해주는 비선형 활성화 함수이다.
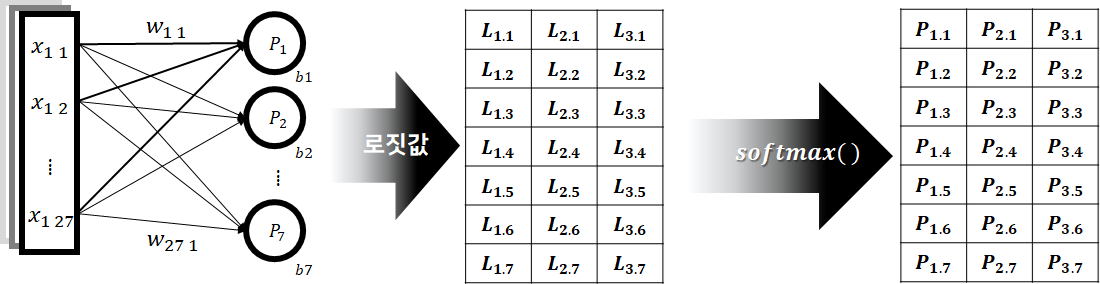
소프트맥스 함수는 ‘기존 상대적 가능성 비율에서 확률값으로 전환시켜 주는 역할’을 수행하고 있다.

소프트맥스 함수의 식이 앞서 살펴본 시그모이드 함수와 비슷하게 생겼다는걸 알 수 있다. 즉 시그모이드 함수가 갖고 있었던 오버플로우 문 제 또한 소프트맥스에서도 발생할 수 있다는 것 이다.
소프트맥스 함수에 입력 벡터 $x_1, x_2, \cdots ,x_n$이 주어졌을 때, 각 𝑥𝑖의 로짓값에 대응하는 확률 𝑦는 $e^{x_i}$ 에 비례하는 값인 $y= e^{x_i}$이 됩니다. 이때 비례상수를 𝑘라고 하면 $y= ke^{x_i}$가 됩니다.
여기서 비례상수란?
어떠한 비율을 실제값으로 결정짓게하는 상수로서 일반적으로 𝑘를 사용한다.
전체 경우의 확률 합은 1이 되어야 하기에 $ke^{x_1} + ke^{x_2} + \cdots + ke^{x_n} = 1$이고, 이 식을 𝑘에 대하여 정리하면 $k = \frac{1}{e^{x_1} + e^{x_2} + \cdots + e^{x_n}}$ 이 된다.
위의 식을 통해 𝑦를 구하는 식은 $y = \frac{e^{x_i}}{e^{x_1} + e^{x_2} + \cdots + e^{x_n}}$ 이 된다.

Softmax 변형식
시그모이드 함수의 $e^{x_i}$ 를 계산하는 과정에서 범위의 제약이 없는 𝑥가 들어오게 되면 값이 매우 커지게 되며 오버플로우 오류가 발생할 가능성이 생기게 된다.
또한 모든 값이 절대값이 아주 큰 음수로 쏠리게 되면 분자와 분모가 모두 0에 수렴하게 되며 결과적으로 0으로 나눗셈을 진행하는 상황이 발생하게 된다.
그래서 이러한 두 가지 문제점을 동시에 해결할 수 있는 방법으로 $x_i$ 의 최댓값을 $x_k$ 라 할 때 소프트맥스 정의식에서 분자와 분모를 동시에 $e^{x_k}$ 로 나누는 방법이 이용되고 있다.
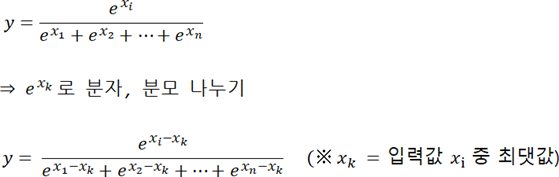
만약 임의의 𝑗 에 대하여 $x_k - x_j \geq 0$ 이므로 $0 < e^{x_k-x_j} \leq 1$ 이 된다.
즉 분자와 분모에 존재하는 값이 모두 0에서 1 사이의 값이 된다는 것이며, 분자와 분모의 어느 항도 지나치게 커질 수 없게 되며 자연스럽게 오버플로우 문제가 사라지게 된다.

Softmax 편미분
소프트맥스 함수는 벡터를 입력으로 받아 벡터를 출력한다. 이 때문에 벡터 성분 간의 편미분이 일대일 혹은 다대일의 구조가 아닌 다대다의 관계가 되면서 편미분 과정이 상당히 복잡하게 된다. 다행인 점은 이러한 소프트맥스의 편미분 계산 과정은 딥러닝 학습에 거의 이용되지 않는다. 그 이유는 시그모이드 함수와 같은 이유로, 막상 편미분 대상은 소프트맥스함수가 아닌 손실 함수를 구해주는 소프트맥스교차 엔트로피이기때문이다.
소프트맥스 함수의 계산 과정에서 입력 벡터 $x_1, x_2, \cdots ,x_n$의 모든 $x_i$는 출력 벡터 $y_1, y_2, \cdots ,y_n$ 의 $y_j$ 에 영향을 미치게 돤다. 즉 소프트맥스 편미분은 모든 $(x_i, y_j)$ 쌍에 대해 구해져야 한다. 따라서 모든 입출력 벡터의 모든 원소 쌍에 대한 편미분 $\frac{\partial y_j}{\partial x_i}$ 값들로 구성된 2차원 행렬을 구해야 한다. 이렇게 다변수 벡터 함수의 도함수 행렬을 야코비 행렬(𝐽𝑎𝑐𝑜𝑏𝑖𝑎𝑛 𝑀𝑎𝑡𝑟𝑖𝑥)이라 한다.
딥러닝 알고리즘은 미니배치 단위로 한꺼번에 여러 개의 데이터를 처리하기에 전체적으로 3차원 텐서의 모습으로 계산된다. 우선 우리는$(x_i, y_j)$ 쌍에 대한 편미분을 구해야 한다. 이 과정에서 $x_i, y_j$ 즉 (𝑖, 𝑗)는 서로 같은 벡터 이거나 혹은 서로 다른 벡터값을 갖게 된다. 그렇다면 편미분 또한 𝑖 ≠ 𝑗, 𝑖 = 𝑗 이렇게 두 경우로 하여 편미분을 구할 수가 있게 된다.
결과적으로 𝑖 ≠ 𝑗의 경우 $\frac{\partial y_j}{\partial x_i} = -y_iy_j$ 로구해지며,
𝑖 = 𝑗 의 경우 $\frac{\partial y_j}{\partial x_i} = y_i - y_i^{2}$ 로구해진다.
Softmax Cross Entropy
두 확률 분포 사이의 교차 엔트로피는 아래와 같은 수식으로 정의할 수 있다.
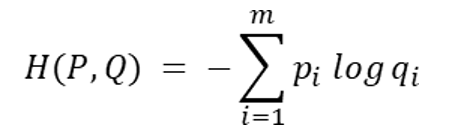
로짓 벡터 $a_1, \cdots , a_n$ 과 정답 벡터 $y_1, \cdots , y_n$이 주어졌다고 할 때, 교차 엔트로피 𝐻(𝑃, 𝑄)를 구하려면 정답 벡터 $y_1, \cdots , y_n$ 을 확률분포 𝑃로 삼고 로짓벡터 $a_1, \cdots , a_n$ 에 소프트맥스 함수를 적용하여 얻어낸 확률 분포를 𝑄로 삼아 교차 엔트로피 정의식에 따라 계산하면 된다.
이 과정에서 신경망의 추론 부분인 𝑄는 로짓 벡터에 소프트맥스 함수를 적용한 결과이기에 확률의 형태로 값이 출력되며, 모든 원소값이 항상 0보다 크고 1보다 작은값을 갖게된다.
아무런 문제가 없어보이지만 여기에는 한가지 문제가 존재한다. 만약 신경망의 연산결과를 통해 얻어진 로짓값 자체가 매우 작은 값을 갖게 된다면 자연스럽게 확률값이 매우 작아져 0에 가까운 값이 될 수 있다. 그리고 표현범위의 문제로 인해 0이 아닌 경우에도 0으로 표현되는 경우까지 발생할 수 있다. 그렇게 되면 로그 함수에서 출력되는 결괏값은 −𝑖𝑛𝑓 로, 또 다시 값이 폭주하는 현상을 불러일으키게 된다.
이러한 문제의 해결책으로 아주 작은 양수값($\varepsilon $)을 도입하여 식을 재정의 해준다.

이렇게 작은 값을 넣어 계산을 진행하게 되면, 어지히 큰 $q_i$ 값에 대해서는 아주 작은 차이를 가져오고, 반대로 0에 매우 가까운 $q_i$ 의 경우에는 일정 값으로 내려가지 못하게 하한선 역할을 수행하며 계산의 폭주를 막아주게 된다.
신경망이 추정한 로짓 벡터 $x_1, \cdots , x_n$ 은 계속 이야기를 하였듯 소프트맥스 함수를 통과시켜 추정확률 분포 $q_1, \cdots , q_n$로 변환할 수 있다. 그리고 정답에 의해 표현되는 확률 분포는 $p_1, \cdots , p_n$ 이므로 소프트맥스 교차 엔트로피는 아래와 같이 정리할 수 있었다.
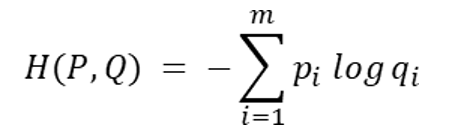
교차 엔트로피의 편미분은 입력값 𝑥 에 따른 소프트맥스의 확률분포 𝑞 의 체인 룰을 적용하여 구할 수가 있게 된다.
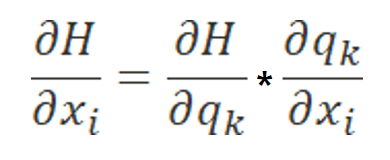
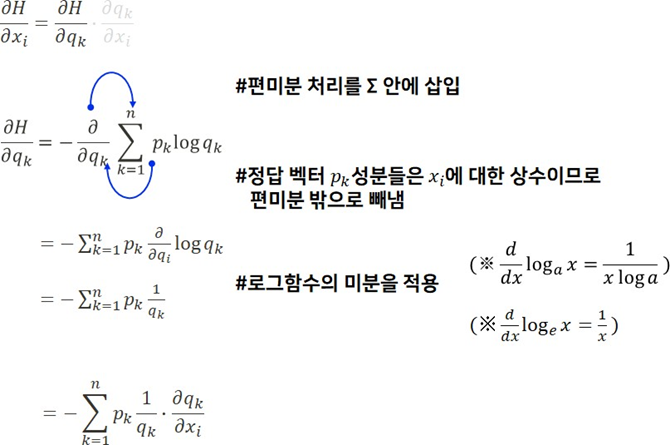
소프트맥스 함수의 편미분 과정에서 𝑖 = 𝑘, 𝑖 ≠ 𝑘 일 때 계산식이 서로 다르다는 걸 확인했다.
그런데 전체 확률값의 합은 아래와 같이 1이 되므로 이것을 고려하여 식을 최종적으로 정리하게 되면 $q_i - p_i$ 라는 값을 얻어낼 수 있게 된다.
우리는$\frac{\partial H}{\partial x_i }$ 의 값이 𝑥 가 아닌 소프트맥스를 통과한 추정 확률 분포 𝑞 와 그저 정답에 의해 표현되는 벡터인 𝑝 의 차이로 구할 수가 있었다.

'DL(Deep-Learning) > 개념' 카테고리의 다른 글
| [실습] numpy로 만드는 다층 신경망 (0) | 2022.01.29 |
|---|---|
| [실습] numpy로 만드는 단층 신경망 - 다중 분류2 (0) | 2022.01.29 |
| [실습] numpy로 만드는 단층 신경망 - 이진 분류 2 (0) | 2022.01.29 |
| [실습] numpy로 만드는 단층 신경망 - 이진 분류 1 (0) | 2022.01.29 |
| train/test/validation 나누기 - splitfolders (0) | 2022.01.29 |
![[실습] numpy로 만드는 단층 신경망 - 다중 분류1](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FbTU7eS%2Fbtrr4ShB4SE%2FAAAAAAAAAAAAAAAAAAAAAJOsChwltalP3NRKJcoDr8Ddmv5-t4L2ZeYDTKeaDFni%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1764514799%26allow_ip%3D%26allow_referer%3D%26signature%3DnUQBYO7waPfi9o17DejyafkCeWA%253D)