우리는 이진 분류 문제를 예측하는 단층 신경망을 만들어 볼 것이다.
이진 분류 문제에서는 Pulsar 데이터를 가지고 별인지 펄서인지 예측하는 신경망을 구축해 볼 예정이다.
데이터 셋은 Kaggle에 있는 Pursar dataset 에서 받아서 사용 할 수 있다.
✔︎ 데이터 살펴보기
import numpy as np
import pandas as pd
df = pd.read_csv('data/pulsar_stars.csv')

총 8개의 독립변수와 하나의 종속변수로 약 17800여개의 데이터셋이 준비되어 있다.
📍 이진 단층 신경망을 만들기 위한 설계도


1. 모듈 불러오기
import numpy as np
import csv
# 실험 결과를 재현하기 위해 난수 발생패턴을 고정시키는 np.random.seed()함수값을 설정
np.random.seed(333)
2. 하이퍼 파라미터 설정
- learning rate 학습률
- 정규분포 난숫값 [ 평균 / 표준편차 ]
RND_MEAN = 0 # 평균
RND_STD = 0.003 # 표준편차
Learning_rate = 0.003 # 학습률
처음에는 이값을 무작위로 지정할 수 밖에 없다.
그렇다면 무작정 무작위값을 주기 보다, 랜덤하지만 적어도 최소한의 규칙성이 있는 범위 내에서 난수를 지정하는 것 이 더 좋을 것 이다.
이러한 방법은 Xavier 초기화 와 He 초기화라 하며 현재 가장 많이 쓰이는 방법이다.
3. 메인함수 정의
def binary_classification_exec(epoch_count=10, mb_size=10, report=1,train_rate = 0.8):
binary_load_dataset()
init_model()
train_and_test(epoch_count, mb_size, report, train_rate)
메인 함수 binary_classification_exec() 함수를 실행하게 되면
#1 데이터를 불러들이는 binary_load_dataset() 함수,
#2 가중치와 편향을 초기화 해주는 init_model() 함수,
#3 학습 및 신경망 성능 테스트를 위한 train_and_test()함수
이렇게 세가지 함수가 차례로 실행되며, 신경망 모델을 생성하고 학습 전체 과정을 일괄 처리한다.
4. 데이터를 불러오는 binary_load_dataset() 정의
# 데이터 받기 > 버퍼로 옮겨주기 > np.array()로 감싸주기
def binary_load_dataset():
with open('/content/pulsar_stars.csv') as csvfile:
csvreader = csv.reader(csvfile)
next(csvreader, None)
rows = []
for row in csvreader:
rows.append(row)
global data, input_cnt, output_cnt
input_cnt, output_cnt = 8, 1 # 독립변수, 종속변수독립변수, 종속변수
data = np.asarray(rows, dtype='float32') # 배열 구조로 변환하는 과정
데이터를 자세히 살펴보면 오직 실수로된 데이터만 존재한다.
원-핫 벡터 표현과정은 생략할 수 있고, 독립변수 input_cnt과 종속변수 output_cnt은 각 8,1의 값을 가진다.
target_class는 0과 1의 값만을 갖고 있는 이진 분류 데이터셋이라는 것을 확인 할 수 있다.
리스트 구조로 되어있는 변수를 asarray 배열 구조로 변환하게 되면 numpy에서 제공하는 다양한 산술 연산과정을 효율적으로 사용할 수 있게된다.
5. 파라미터 초기화 함수 init_model() 정의
def init_model():
global weight, bias, input_cnt, output_cnt
weight = np.random.normal(RND_MEAN, RND_STD,[input_cnt, output_cnt])
# normal 메서드 : (mean, sd, shape)
bias = np.zeros([output_cnt])
# weight 가중치 행렬은 [8,1] , bias 편향 벡터는 [1]형태
6. 학습 및 평가 함수 train_and_test() 정의
def train_and_test(epoch_count, mb_size, report, train_rate):
step_count = arrange_data(mb_size, train_rate)
test_x, test_y = get_test_data()
for epoch in range(epoch_count):
losses, accs = [], []
for n in range(step_count):
train_x, train_y = get_train_data(mb_size, n)
loss, acc = run_train(train_x, train_y)
losses.append(loss)
accs.append(acc)
if report > 0 and (epoch + 1) % report == 0:
acc = run_test(test_x, test_y)
print(f'Epoch {epoch+1}: loss={np.mean(losses):5.3f}, accuracy={np.mean(accs):5.3f}/{acc:5.3f}')
final_acc = run_test(test_x, test_y)
print(f'\nFinal Test: final accuracy = {final_acc:5.3f}')
train_and_test() 안에 정의된 함수
- arrange_data()
- get_train_data()
- get_test_data()
- run_train()
- run_test()
def arrange_data(mb_size, train_rate):
global data, shuffle_map, test_begin_idx
shuffle_map = np.arange(data.shape[0])
np.random.shuffle(shuffle_map)
step_count = int(data.shape[0] * train_rate) // mb_size
test_begin_idx = step_count * mb_size
return step_count
def get_test_data():
global data, shuffle_map, test_begin_idx, output_cnt
test_data = data[shuffle_map[test_begin_idx:]]
return test_data[:, :-output_cnt], test_data[:, -output_cnt:]
def get_train_data(mb_size, nth):
global data, shuffle_map, test_begin_idx, output_cnt
if nth == 0:
np.random.shuffle(shuffle_map[:test_begin_idx])
train_data = data[shuffle_map[mb_size * nth:mb_size * (nth + 1)]]
return train_data[:, :-output_cnt], train_data[:, -output_cnt:]
def run_train(x, y):
output, aux_nn = forward_neuralnet(x)
loss, aux_pp = forward_postproc(output, y)
accuracy = eval_accuracy(output, y)
G_loss = 1.0
G_output = backprop_postproc(G_loss, aux_pp)
backprop_neuralnet(G_output, aux_nn)
return loss, accuracy
def run_test(x, y):
output, _ = forward_neuralnet(x)
accuracy = eval_accuracy(output, y)
return accuracy
7. 순전파 및 역전파 함수 정의
7.1 신경망의 순전파 연산과정 forward_neuralnet()
def forward_neuralnet(x):
global weight, bias
output = np.matmul(x, weight) + bias # y = xw + b
return output, x
7.2 역전파 파라미터 갱신 backprop_neuralnet()
def backprop_neuralnet(G_output, x):
global weight, bias
g_output_w = x.transpose()
G_w = np.matmul(g_output_w, G_output)
G_b = np.sum(G_output, axis=0)
weight -= LEARNING_RATE * G_w
bias -= LEARNING_RATE * G_b평균제곱오차의 각 단계별 입출력 간 부분적인 기울기를 구해놓고, 손실에 대한 기울기의 연쇄적 계산에 활용하여 최종적으로 mse의 역전파 처리인 G_output을 계산하였다.
7.3 순전파 수행 함수 forward_postproc()
def forward_postproc(output, y):
CEE = sigmoid_cross_entropy_with_logits(y, output)
loss = np.mean(CEE)
return loss, [y, output, CEE]
여기서 새로운 함수인 sigmoid_cross_entropy_with_logits() 가 등장하는데, 이 함수의 경우 앞서 살펴본 개선된 시그모이드 교차 엔트로피 함수이다.
def sigmoid_cross_entropy_with_logits(z, x):
return relu(x) - x * z + np.log(1 + np.exp(-np.abs(x)))
신경망 연산 결과인 output과 종속변수(y)를 바탕으로 로짓값 해석, 시그모이드 함수, 교차 엔트로피 이 과정을 거쳐 CEE 를 계산한다. 그리고 구해진 값들에 대해 평균을 내어 𝑙𝑜𝑠𝑠 값을 계산한다.
return 을 통해 loss와 [y, output, CEE] 를 반환하는데, 하나의 리스트를 반환하는 이유는 순전파의 손실함수를 구하는 과정이었던 forward_postproc()에서 구한 값을 바탕으로 역전파를 수행하기 위해 [y,output,CEE] 를 반환한다.
7.4 역전파 수행 함수 정의 backprop_postproc()
def backprop_postproc(G_loss, aux):
y, output, entropy = aux
g_loss_entropy = 1.0 / np.prod(entropy.shape)
g_entropy_output = sigmoid_cross_entropy_with_logits_derv(y, output)
G_entropy = g_loss_entropy * G_loss
G_output = g_entropy_output * G_entropy
return G_output
손실함수에 대한 과정을 역전파 하는 단계
이 함수의 순전파 과정에서 얻어진 y, output, CEE를 인자 aux로 받아와 이 값들에 영향을 미친 모든 과정에 대한 역전파 과정을 살펴보자.
다시 손실 함수의 과정을 역으로 살펴보면 손실, 평균, 교차엔트로피, 시그모이드 이렇게 단계를 나눠볼 수 있다.
이 과정에서 손실과 평균을 제외하고 교차 엔트로피에 대한 편미분 과정을 정의하다 보니 자연스럽게 시그모이드 과정 또한 정의되었고, 그 식을 바탕으로 시그모이드의 교차엔트로피에 대한 편미분 과정을 정의했었습니다.
8. 정확도 계산 eval_accuracy()
def eval_accuracy(output, y):
estimate = np.greater(output, 0)
answer = np.greater(y, 0.5)
correct = np.equal(estimate, answer)
return np.mean(correct)
- 정답을 맞췄는지에 대한 여부를 정확도로 측정
실행하기
binary_classification_exec()

좋은 결과가 나왔지만 이 결과에는 약간의 오류가 숨어있다.
pulsar 데이터에서 마지막 target_class에서 0을 의미하는 일반 별의 분포가 90%를 차지하고 있다.
이렇게 데이터의 균형이 무너지면 정확도를 측정하는 과정에서 문제가 발생한다.
학습이 잘 되지 않아 정답을 출력할 때 무조건 '일반 별'이라고 대답하게 된다.
그럼에도 정확도가 높은 이유는 일반 별의 데이터가 90%를 차지하기 때문이다.
이렇게 데이터의 불균형이 일어났을 때, 데이터의 증폭을 이용하여 pursal 데이터를 늘려서 학습을 진행한다.
정확도가 정확하게 보여지지 않는 상황을 타개하기 위해 신경망의 성능을 더욱 잘 보여줄 수 있는 또 다른 평가지표가 필요하다. 바로 정밀도(precision)와 재현율(recall) 이다.
정밀도와 재현율에 대해서는 여기를 참고하세요.
간단하게 얘기해보면,
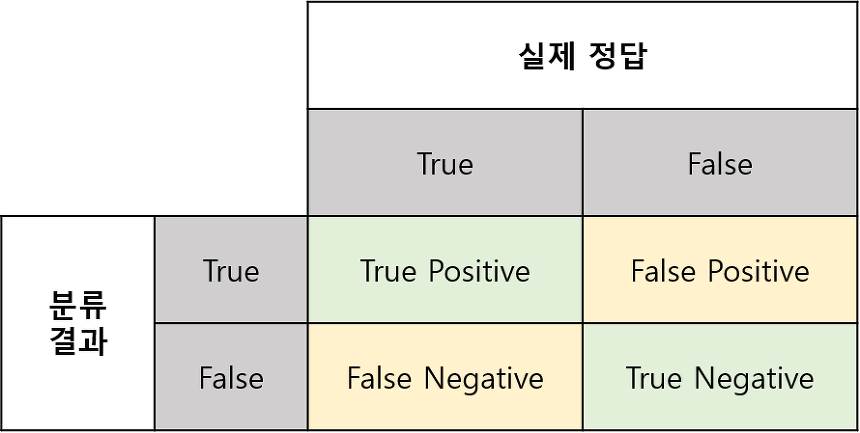
- TP : 신경망의 추측이 '참(P)'이며, 데이터의 정답 또한 '참'(T)으로 정확하게 평가한 결과
- TN : 신경망의 추측이 '거짓(N)'이며, 데이터의 정답은 '참'(T)으로 부정확하게 평가한 결과
- FP : 신경망의 추측이 '참(P)'이며, 데이터의 정답은 '거짓(F)'으로 부정확하게 평가한 결과
- FN : 신경망의 추측이 '거짓(N)'이며, 데이터의 정답 또한 '거짓(F)'으로 정확하게 평가한 결과
Precision(정밀도)
정밀도란 모델이 True라고 분류한 것 중에서 실제 True인 것의 비율
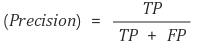
Positive 정답률, PPV(Positive Predictive Value)라고도 불린다.
Recall(재현율)
재현율이란 실제 True인 것 중에서 모델이 True라고 예측한 것의 비율

'정밀도'와 '재현율' 중 하나의 값 만을 높이는 것은 매우 쉽다. 다만 하나의 값만을 높이게 되면 다른 하나의 값이 떨어지게 되는 현상이 발생한다. 우리는 이 두가지 값을 동시에 올려야한다. 이에 따라 정밀도와 재현율의 조화평균인 𝐹1 𝑠𝑐𝑜𝑟𝑒 값이 정확도 대신 사용하기도 한다. 조화평균은 역수의 차원에서 평균을 구하고, 다시 역수를 취해 원래 차원의 값으로 돌아오게 하여 구할 수가 있다.
데이터를 증폭하여 성능 높이기
우리는 이제 몇 가지의 함수를 약간 수정하여 pulsar 데이터를 증폭시키고, 새로운 지표를 통해 현재 단층 퍼셉트론의 성능을 확인해 볼 것이다.
3. 메인함수 정의
def binary_classification_exec(epoch_count=10, mb_size=10, report=1,train_rate = 0.8, adjust_ratio = False):
binary_load_dataset(adjust_ratio)
init_model()
train_and_test(epoch_count, mb_size, report, train_rate)
adjust_ratio 라는 새로운 인자가 등장하였으며, 이 인자는 binary_load_dataset()로 할당되어 진다.
이 인자의 역할은 pulsar 데이터를 증폭시켜주는 역할을 수행하게 됩니다.
4. 데이터를 불러오는 binary_load_dataset() 정의
def binary_load_dataset(adjust_ratio):
pulsars, stars = [], []
with open('data/pulsar_stars.csv') as csvfile:
csvreader = csv.reader(csvfile)
next(csvreader, None)
for row in csvreader:
if row[8] == '1': pulsars.append(row)
else:
stars.append(row)
global data, input_cnt, output_cnt
input_cnt, output_cnt = 8, 1
star_cnt, pulsar_cnt = len(stars), len(pulsars)
# adjust_ratio가 참인 경우 기존 data버퍼 보다 크기를 star_cnt의 2배 만큼 늘려준다
if adjust_ratio:
data = np.zeros([2 * star_cnt, 9])
data[0:star_cnt, :] = np.asarray(stars, dtype='float32')
# 여기서 절반은 기존 star데이터를 담아주며, 나머지 절반에는 pulsar데이터를 담아주는데,
# 이때 반복문 for와 나머지 연산자 %를 통해 pulsar데이터의 범위를 반복해서 data버퍼에 담아준다.
for n in range(star_cnt):
data[star_cnt + n] = np.asarray(pulsars[n % pulsar_cnt],
dtype='float32')
# 만약 adjust_ratio 인자가 False라면 이전 과정과 같이 수행
else:
data = np.zeros([star_cnt + pulsar_cnt, 9])
data[0:star_cnt, :] = np.asarray(stars, dtype='float32')
data[star_cnt:, :] = np.asarray(pulsars, dtype='float32')
8. 정확도 계산 eval_accuracy()
평가를 위한 지표들을 정의하는 단계
def eval_accuracy(output, y):
est_yes = np.greater(output, 0)
ans_yes = np.greater(y, 0.5)
est_no = np.logical_not(est_yes)
ans_no = np.logical_not(ans_yes)
tp = np.sum(np.logical_and(est_yes, ans_yes))
fp = np.sum(np.logical_and(est_yes, ans_no))
fn = np.sum(np.logical_and(est_no, ans_no))
tn = np.sum(np.logical_and(est_no, ans_yes))
accuracy = safe_div(tp+tn, tp+tn+fp+fn)
precision = safe_div(tp, tp+fp)
recall = safe_div(tp, tp+fn)
f1 = 2 * safe_div(recall*precision, recall+precision)
return [accuracy, precision, recall, f1]
def safe_div(p, q):
p, q = float(p), float(q)
if np.abs(q) < 1.0e-20: return np.sign(p)
return p / q
np.greater()의 경우 두 가지 입력값을 받아 두 번째 인자를 기준하여 값이 크면 '참', 작으면 '거짓'을 출력해준다. 이 기능을 통해 신경망의 연산결과인 output과 실제 정답 y를 0 과 비교하여 부호를 알아낼 수 있게된다.
np.logical_not() 함수는 입력값이 '참'일 경우에는 '거짓'을 출력하며, 반대로 입력값이 '거짓'인 경우에는 '참'을 반환하는 매우 단순한 기능을 가지고 있다. 이러한 기능을 통해 앞서 구한 결과의 반대되는 결과를 est_no, ans_no 에 저장하게 된다.
np.logical_and() 함수의 경우 입력값이 모두 True인 경우에만 True를 반환하며 이 기능을 통해 신경망의 추정결과와 실제 정답의 결과를 비교하여 줄 수 있다.
이러한 기능을 통해 각 TN, TP, FN, FP의 수식을 코드로 나타낼 수 있으며 이렇게 구한 결과를 통해 정밀도, 재현율, F1 그리고 정확도를 얻게 될 수 있게된다.
나눗셈을 수행하는 것 대신 safe_div() 라는 함수가 쓰인다.
이 변수의 경우 형변환에 대한 문제, 분모가 0으로 바뀌게되는 문제를 해결해준다.
만약 분모가 매우 작은 값, 즉 0인 경우에 분모를 분자의 부호에 맞는 1 혹은 -1로 변환해 준다. 그럼 분모가 0이되는 경우 값이 1 혹은 -1이 되어 나눗셈의 문제는 사라지게 된다. 여기서 작은값을 나타내기 위해 사용되는 1.0e-20은 과학적 표기법이라 하며, 아주 작은값을 표현한 것이다.
6. 학습 및 평가 함수 train_and_test() 정의
def train_and_test(epoch_count, mb_size, report, train_rate):
step_count = arrange_data(mb_size, train_rate)
test_x, test_y = get_test_data()
for epoch in range(epoch_count):
losses, accs = [], []
for n in range(step_count):
train_x, train_y = get_train_data(mb_size, n)
loss, acc = run_train(train_x, train_y)
losses.append(loss)
accs.append(acc)
if report > 0 and (epoch+1) % report == 0:
acc = run_test(test_x, test_y)
print('Epoch {}: loss={:5.3f}, \n accuracy:{:5.3f}, precision:{:5.3f}, recall:{:5.3f}, f1:{:5.3f}'. \
format(epoch+1, np.mean(losses), acc[0],acc[1],acc[2],acc[3]))
final_acc = run_test(test_x, test_y)
print('\nFinal Test: accuracy:{:5.3f}, precision:{:5.3f}, recall:{:5.3f}, f1:{:5.3f}'.\
format(final_acc[0],final_acc[1], final_acc[2], final_acc[3]))

단순 정확도를 살펴보기 보단, 정밀도와 재현율 그리고 𝐹1 𝑠𝑐𝑜𝑟𝑒를 주의깊게 살펴봐야 한다. 최종 테스트 결과 pulsar 데이터를 증폭시킨 결과에 대한 모든 지표가 더 높은 결괏값을 출력해 내고 있다. 특히 재현율과 더불어 𝐹1 𝑠𝑐𝑜𝑟𝑒가 눈에 띄게 향상되었다는 것을 확인할 수 있다. 하지만 이러한 데이터 증폭 방식을 무작정 적용하게 되면 이후 '과잉적합' 이라는 문제점을 마주하게 되는데 이것은 나중에 알아보도록 하자.
'DL(Deep-Learning) > 개념' 카테고리의 다른 글
| [실습] numpy로 만드는 단층 신경망 - 다중 분류2 (0) | 2022.01.29 |
|---|---|
| [실습] numpy로 만드는 단층 신경망 - 다중 분류1 (0) | 2022.01.29 |
| [실습] numpy로 만드는 단층 신경망 - 이진 분류 1 (0) | 2022.01.29 |
| train/test/validation 나누기 - splitfolders (0) | 2022.01.29 |
| [DL] 엔트로피 Entropy (0) | 2022.01.29 |
![[실습] numpy로 만드는 단층 신경망 - 이진 분류 2](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FbCoVxy%2Fbtrr9gC87dX%2FAAAAAAAAAAAAAAAAAAAAAHSkL6o8dwFymj3wnG-Df-5JiHgq5184awtgAljHPHO_%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1764514799%26allow_ip%3D%26allow_referer%3D%26signature%3DZ7qFOsdJIUXkYIfnhshS239Q624%253D)